一种针对堆栈平板式卫星的刚柔耦合姿态动力学建模方法

本发明实例涉及航天器动力学领域，尤其涉及一类堆栈平板式卫星的刚柔耦合姿态动力学的变分积分方法。

背景技术：

1、近年来卫星互联网星座技术的快速发展，以轻质化、高功能密度化及柔性化为特征的空间系统逐渐成为卫星设计的重要趋势。其中相比于陆基信号基站，用以对地提供网络直连服务的低轨卫星距终端设备较远，立方体卫星通常使用的传统尺寸天线几乎不可能从地面移动终端接收到信号，而模块化设计的超大型相控阵天线阵列可突破这一物理约束。此外卫星天线尺寸与在卫星通信信道中可实现的数据吞吐量直接相关，除增益之外，增加卫星天线尺寸还可提高空间分辨率，从而在给定的服务区域内实现更大的频率复用。因此在同低功率、低信号强度的地面移动终端进行通信时，部署更大的相控阵天线是建设未来太空基站，实现对地移动终端网络直连的必要途径，比如于2022年由美国ast&science研发的bluewalker-3大型手机直连卫星具备近1500kg的质量，其所搭载的相控阵天线达到了64m2。另一方面随着此类卫星电子设备的升级，星载的太阳能阵列在整个卫星的质量、尺寸所占的比重越来越大，因此搭载大功率电子设备的卫星的太阳能阵列通常具有较大的翼展。2019年以来，亚马逊、telesat和spacex等航天企业正致力于部署巨型星座来为全球提供宽带互联网，其中spacex公司所构建的starlink卫星互联网星座中单星的结构设计上采用了平板式的扁平化设计方案，初代的整星产品质量约为240～260kg，太阳翼面积达到24m2，而第二代的产品中也将具备更大的质量和翼展面积。近期我国也开发了一系列的可堆叠平板式卫星产品，譬如2023年发射的灵犀03星、龙江3号等试验星，其旨在为国内未来卫星的批量化制造和大规模部署提供技术支撑。

2、堆栈平板式阵列卫星的大翼展往往具备一定程度的柔性和较低的固有频率。保证卫星动力学高保真度的关键在于对易弯曲或振动的附件进行建模，如相控阵天线阵列和太阳能阵列。此类大尺寸附件在复杂空间环境中易于弯曲，多数情况下，柔性附件的弯曲需要包含在整星的动力学模型中。初始建模过程中，一般假设卫星为刚体，但若存在柔性附件，该假设会降低数值仿真的保真度。尽管现阶段已有多种柔性体离散化方法，包括假设模态法、有限元法、有限段法和无网格法，但此类动力学模型维数通常较高，通常计算量大、耗时长。

3、工程应用中通常采用单位四元数来表征姿态，其数值积分过程中一般在每一积分步中通过归一化来施加单位长度的约束，这种方法并不利于几何结构的保持和动量、能量的守恒。通过基于旋转矩阵的姿态表征方式和变分积分器可以解决这一问题，但同时引入了过多的姿态表征参数，占用了较多的计算资源，算法的实现成本较高。

技术实现思路

1、针对现有堆栈平板式阵列卫星采用旋转矩阵的姿态表征方式存在冗余表征的问题，本发明提供一种针对堆栈平板式卫星的刚柔耦合姿态动力学建模方法。该方法使用单位四元数推导了用于堆栈平板式卫星的李群变分积分器，该积分器全局有效，避免了旋转矩阵的冗余表征弊端，此外，这种方式推导的积分法保留了连续系统的许多特性，例如动量和能量守恒。

2、本发明所述一种针对堆栈平板式卫星的刚柔耦合姿态动力学建模方法，该方法包括以下步骤：

3、步骤1、建立惯性坐标系卫星体坐标系和板式附件浮动坐标系

4、步骤2、根据各坐标系分别建立卫星各附件质量元素相对卫星体坐标系的位置、速度关系；

5、步骤3、根据整星姿态运动学方程及板式附件的振动姿态运动学方程获取整星姿态四元数变分、振动姿态四元数变分、卫星体坐标系下整星的质心位置向量、整星质心位置向量的一阶导数及整星质心位置向量的变分；

6、步骤4、获取整星的动能、势能及其变分，并根据实际非保守力、力矩获取虚功的表达式；

7、步骤5、根据连续系统的largrange量获取离散系统的largrange量；

8、步骤6、根据离散legendre变换建立整星离散hamilton动力学方程，完成堆栈平板式卫星的刚柔耦合姿态动力学建模。

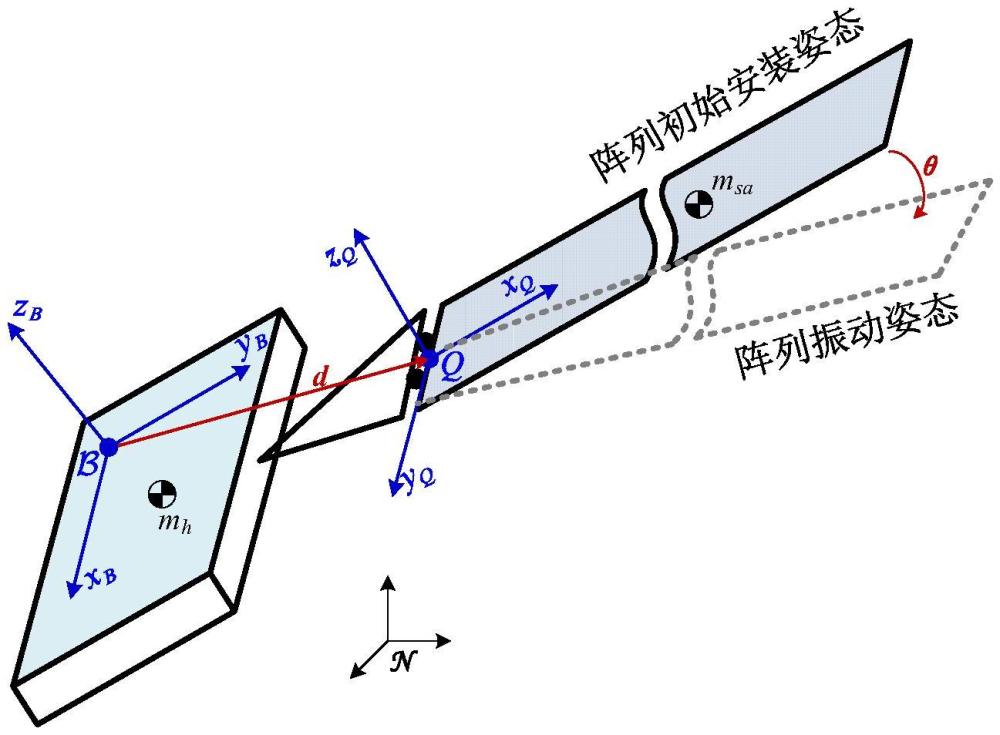
9、优选地，步骤1中的卫星体坐标系的原点位于卫星轮毂上的任意位置；

10、附件浮动坐标系的原点位于板式附件与轮毂的铰接点处，三轴xqyqzq与附件固连，轴指向翼展伸展方向，轴垂直于翼平面，轴由右手定则给定，附件浮动坐标系用于表征卫星板式附件偏离初始安装姿态的振动姿态。

11、优选地，步骤2包括轮毂上任一质量元素的位置向量、速度和板式附件上任一质量元素的位置向量、速度；

12、其中，轮毂上任一质量元素的位置向量rh、速度vh按下式获取：

13、

14、式中为卫星体坐标系原点至轮毂质心的向量，在系下表示；r为卫星相对惯性坐标系的姿态矩阵，ω为卫星相对惯性坐标系的角速度；ρ为轮毂质心至该质量元素的位置向量；

15、板式附件上任一质量元素的位置向量rsa、速度vsa按下式获取：

16、

17、式中rh为板式附件相对卫星体坐标系的初始安装姿态；d为卫星体坐标系原点至板式附件浮动坐标系原点的向量，在系下表示；s为板式附件浮动坐标系原点至板式附件质心的向量；rsa为板式附件偏离其安装姿态的振动姿态；ρsa为板式附件质心至板式附件上该质量元素的位置向量；θ为板式附件绕轴的振动角；为板式附件绕轴的振动角速度；e2表示轴单位向量，

18、优选地，步骤3具体包括：

19、步骤31、根据整星姿态运动学方程获取整星姿态四元数变分；

20、整星姿态运动学方程为：

21、

22、式中表示四元数乘法，q表示整星的姿态四元数，表示整星的姿态四元数导数，表示整星角速度的增广纯四元数表示，且

23、根据整星姿态运动学方程获取整星四元数变分为：

24、

25、式中δ[·]表示·的变分，ε表示无穷小变化量，表示四元数指数，表示η的增广纯四元数，η表示姿态无穷小变分；

26、步骤32、根据板式附件的振动姿态运动学方程获取振动姿态四元数变分；

27、板式附件的振动姿态运动学方程为：

28、

29、式中qsa表示板式附件相对卫星体坐标系的振动姿态四元数，表示板式附件相对卫星体坐标系的振动姿态四元数导数，表示轴单位向量的增广纯四元数；

30、根据板式附件的振动姿态运动学方程获取振动姿态四元数变分为：

31、

32、根据可推导得到角速度变分：

33、

34、步骤33、获取卫星体坐标系下整星的质心位置向量csc：

35、

36、式中，msa、mh、msc分别为板式附件质量、轮毂质量和整星质量；

37、步骤34、根据板式附件的振动姿态运动学方程计算整星的质心位置一阶导数：

38、

39、[·]^表示3维向量到3×3斜对称矩阵的映射；

40、步骤35、获取整星质心位置向量的变分：

41、

42、优选地，步骤4具体包括：

43、步骤41：计算整星动能：

44、

45、式中表示·的矩阵转置，

46、vh表示轮毂体积，vsa表示板式附件体积，

47、a表示整星转动惯量，为轮毂相对于卫星体坐标系的转动惯量；jh为轮毂相对于轮毂质心的转动惯量；为板式附件相对系的转动惯量；jsa为板式附件相对其质心的转动惯量；th为轮毂动能；tsa为板式附件动能；

48、步骤42：计算整星势能：

49、

50、式中r为惯性坐标系到卫星体坐标系的位置向量，μ为行星引力常数；uh表示轮毂势能；usa表示板式附件势能；

51、步骤43：计算整星势能的变分：

52、

53、步骤44：考虑非保守力其中fc为控制力，关于空间环境扰动力fd仅考虑卫星体坐标系下的j2摄动力

54、

55、式中表示j2摄动加速度，rx ry rz分别表示惯性坐标系下卫星的三轴位置标量，j2为摄动系数，为地球行星平均半径；

56、非保守外力虚功按下式计算：

57、δwex＝fnc·δrsc+τc·η

58、式中rsc为卫星体坐标系下整星质心位置矢量，τc表示卫星控制力矩；

59、非保守内力虚功按下式计算：

60、

61、式中k为扭簧的弹簧系数；c为扭转阻尼系数；

62、由此系统总虚功按下式获取：

63、

64、式中τsa表示板式附件受到的外力矩，τsc表示整星受到的外力矩，

65、优选地，步骤5具体包括：

66、步骤51：根据整星动能t和势能u获取连续系统largrange量l为：

67、

68、式中msc＝mh+msa；

69、步骤52：根据步骤51的连续系统largrange量l计算离散系统largrange量ld，具体步骤包括：

70、对各速度项离散化：

71、

72、式中，h表示固定积分步长，[·]k、[·]k+1表示tk、tk+1时刻的变量·；

73、im(·)表示四元数的向量部分，[·]*表示·的共轭四元数；

74、则离散系统largrange量表达为：

75、

76、式中，ld(qk,θk,qk+1,θk+1)表示tk时刻至tk+1时刻的离散系统largrange量，l(qk,θk,qk+1,θk+1)表示tk时刻的连续系统largrange量；

77、步骤53、依据非保守体系下的离散legendre变换公式，推导离散hamilton动力学方程：

78、上式中，pk、pk+1分别表示tk时刻和tk+1时刻的广义动量，τk、τk+1分别表示tk时刻和tk+1时刻的广义力矩，ld(qk,qk+1)表示广义离散largrange量；

79、获取离散hamilton动力学方程为：

80、

81、

82、对任意四元数ξs、ξv分别表示四元数ξ的标量和向量部分且

83、式中，分别表示tk时刻和tk+1时刻的整星角动量和板式附件振动角动量；

84、rsa,k表示tk时刻整星姿态矩阵；

85、τsc,k、τsc,k+1分别表示tk时刻和tk+1时刻的整星受到的外部力矩；

86、τsa,k、τsa,k+1分别表示tk时刻和tk+1时刻的板式附件受到的外部力矩；

87、qs、qv分别表示四元数q的标量和向量部分；

88、i3表示3×3单位矩阵；

89、δθk表示tk时刻至tk+1时刻的角位移增量，且δθk＝θk-1-θk；

90、fk表示tk时刻至tk+1时刻的整星姿态增量四元数，且

91、本发明的有益效果：

92、1.四元数变分积分器表现出真实的能量和动量行为，同时计算成本与低阶龙格-库塔方法相当，适用于卫星的仿真模拟、实时估计和控制应用；

93、2.该方法同时考虑了卫星在轨运行时姿态与板式结构附件振动间的相互耦合作用，动力学模型的保真度得到了保证；

94、3.不同于以往质心固定的假设，该模型考虑了整星质心的时变特性，所获得的动力学模型更为精确。